NewtonPlus - A Fast Big Number Square Root Function
A fast, possibly the fastest, square root function for Big Integers and Floats in C# and Java.
A Fast square root function for Big Integers and floats. The algorithm uses a variety of new and existing ideas to calculate the square root with greater efficiency and better performance than other algorithms. The performance of this function only starts to stand out for numbers above 252. It is presented in both Java and C# versions.
Contents
Introduction
Below is a fast square root function for big integers and floats. The algorithm uses a variety of new and existing ideas to calculate the square root with greater efficiency and better performance than other algorithms. The performance of this function only starts to stand out for numbers above 5 × 1014 (or 252).
The algorithm consists of a core integer square root function and a wrapper for BigFloats.
Integer version - This function rounds down to the nearest integer (floor).
BigFloats / Real number wrapper – An adapter for the Integer version that adds floating point and optional precision.
The integer square root function has been extensively tested with various test types and benchmarks.
C# Version
Performance Benchmarks
Benchmarks have been done on this algorithm throughout its development. The benchmarks were first to compare against others and later to compare against my own versions. Since there is such a wide range in performance, log scale charts are used for comparisons. Please note that small differences equate to large performance differences. Some Big-O examples have been added as color bands for X3, X2 × Log(X), and X2. These bands all converge at 0,0, but the bottom of the chart has been removed for better visibility.
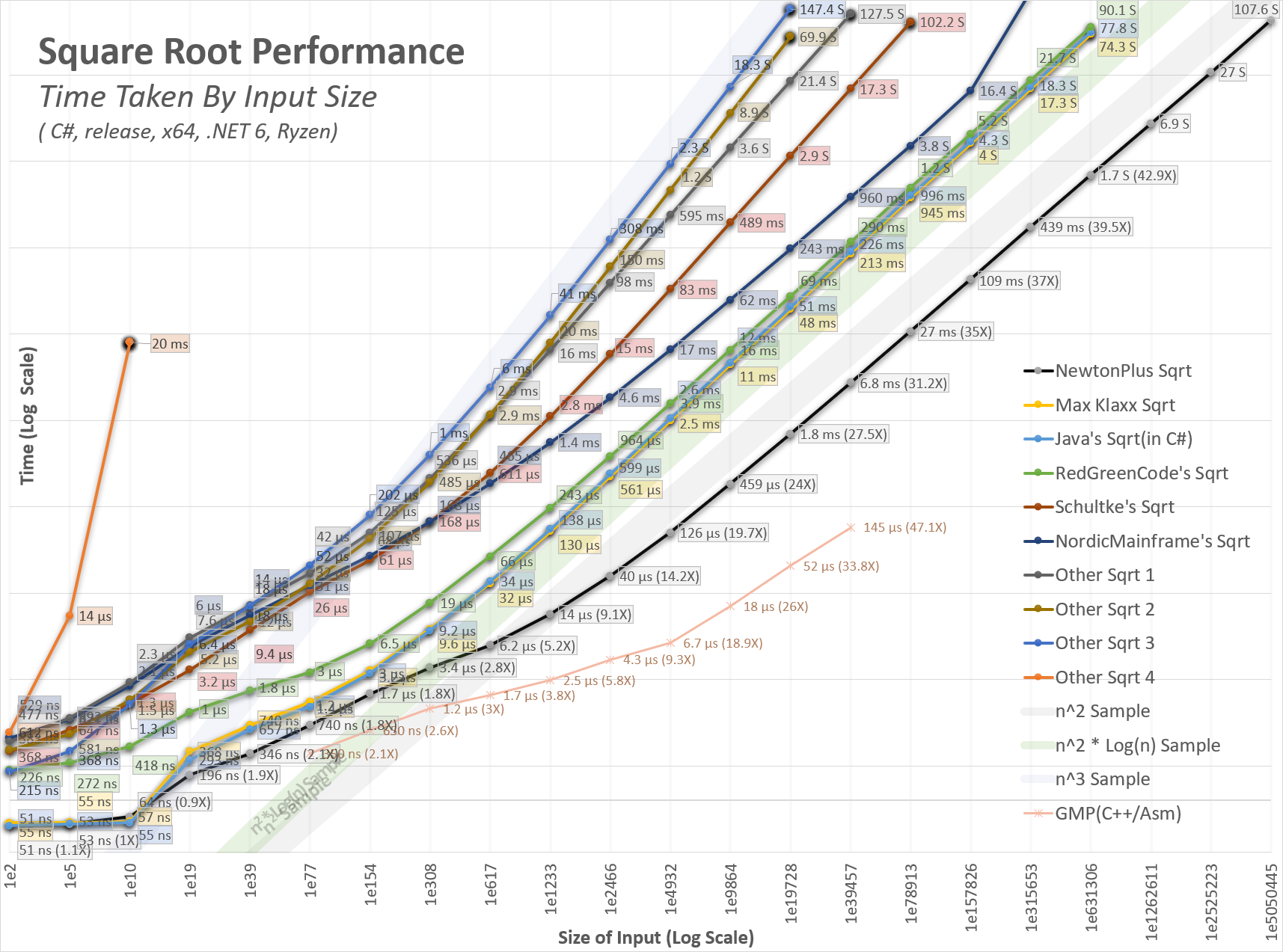
For the functions tested, there seemed to be four classes of performance. The time examples are from my test workstation and will vary slightly with different hardware.
Big O(cn) – These take the longest to run for large numbers. A 40,000-digit binary number would translate to around 1e6000 years. These are not shown in the above chart.
Big O(n3) – These are much faster than the O(cn) algorithms. A 40,000-digit binary number would translate to 500 seconds.
Big O(n2 × log(n)) – These are the much faster and more thought-out algorithms. A 40,000-digit binary takes around just 230ms.
Big O(n2) – This project is consistent with this band or maybe even slightly faster. A 40,000-digit binary number takes around 8ms.
The Code (C# Version)
Just show me the code, will you?
public static BigInteger NewtonPlusSqrt(BigInteger x)
{
if (x < 144838757784765629) // 1.448e17 = ~1<<57
{
uint vInt = (uint)Math.Sqrt((ulong)x);
if ((x >=4503599761588224) && ((ulong)vInt * vInt > (ulong)x)) //4.5e15 =~1<<52
{
vInt--;
}
return vInt;
}
double xAsDub = (double)x;
if (xAsDub < 8.5e37) // 8.5e37 is V²long.max * long.max
{
ulong vInt = (ulong)Math.Sqrt(xAsDub);
BigInteger v = (vInt + ((ulong)(x / vInt))) >> 1;
return (v * v <= x) ? v : v - 1;
}
if (xAsDub < 4.3322e127)
{
BigInteger v = (BigInteger)Math.Sqrt(xAsDub);
v = (v + (x / v)) >> 1;
if (xAsDub > 2e63)
{
v = (v + (x / v)) >> 1;
}
return (v * v <= x) ? v : v - 1;
}
int xLen = (int)x.GetBitLength();
int wantedPrecision = (xLen + 1) / 2;
int xLenMod = xLen + (xLen & 1) + 1;
//////// Do the first Sqrt on hardware ////////
long tempX = (long)(x >> (xLenMod - 63));
double tempSqrt1 = Math.Sqrt(tempX);
ulong valLong = (ulong)BitConverter.DoubleToInt64Bits(tempSqrt1) & 0x1fffffffffffffL;
if (valLong == 0)
{
valLong = 1UL << 53;
}
//////// Classic Newton Iterations ////////
BigInteger val = ((BigInteger)valLong << (53 - 1)) + (x >> xLenMod - (3 * 53)) / valLong;
int size = 106;
for (; size < 256; size <<= 1)
{
val = (val << (size - 1)) + (x >> xLenMod - (3 * size)) / val;
}
if (xAsDub > 4e254) // 1 << 845
{
int numOfNewtonSteps = BitOperations.Log2((uint)(wantedPrecision / size)) + 2;
////// Apply Starting Size ////////
int wantedSize = (wantedPrecision >> numOfNewtonSteps) + 2;
int needToShiftBy = size - wantedSize;
val >>= needToShiftBy;
size = wantedSize;
do
{
//////// Newton Plus Iterations ////////
int shiftX = xLenMod - (3 * size);
BigInteger valSqrd = (val * val) << (size - 1);
BigInteger valSU = (x >> shiftX) - valSqrd;
val = (val << size) + (valSU / val);
size *= 2;
} while (size < wantedPrecision);
}
/////// There are a few extra digits here, lets save them ///////
int oversidedBy = size - wantedPrecision;
BigInteger saveDroppedDigitsBI = val & ((BigInteger.One << oversidedBy) - 1);
int downby = (oversidedBy < 64) ? (oversidedBy >> 2) + 1 : (oversidedBy - 32);
ulong saveDroppedDigits = (ulong)(saveDroppedDigitsBI >> downby);
//////// Shrink result to wanted Precision ////////
val >>= oversidedBy;
//////// Detect a round-ups ////////
if ((saveDroppedDigits == 0) && (val * val > x))
{
val--;
}
// //////// Error Detection ////////
// // I believe the above has no errors but to guarantee the following can be added.
// // If an error is found, please report it.
// BigInteger tmp = val * val;
// if (tmp > x)
// {
// throw new Exception("Sqrt function had internal error - value too high");
// }
// if ((tmp + 2 * val + 1) <= x)
// {
// throw new Exception("Sqrt function had internal error - value too low");
// }
return val;
}Floating Point Version / Adapter
With this project, I also wanted to make a BigFloat version for large floating points. To do this, a few BigFloat versions were constructed from scratch. Despite this, all that was needed was a simple wrapper function for the BigInteger version. BigFloat and BigInteger versions are roughly the same. An encapsulating function, shown below, simply adds some spice to the BigInteger version to track the precision and shifts.
(BigInteger val, int shift) SunsetQuestSqrtFloatUsingIntVersion
(BigInteger x, int shift = 0, int wantedPrecision = 0)
{
int xLen = (int)x.GetBitLength();
if (wantedPrecision == 0) wantedPrecision = xLen;
if (x == 0) return (0, wantedPrecision);
int totalLen = shift + xLen;
var needToShiftInputBy = (2 * wantedPrecision - xLen) - (totalLen & 1);
var val = SunsetQuestSqrt(x << needToShiftInputBy);
var retShift = (totalLen + ((totalLen > 0) ? 1 : 0)) / 2 - wantedPrecision;
return (val, retShift);
}
The pre/post calculations are relatively simple. In a nutshell, the precision we get out of the Sqrt function is half what we put in. So, if we want 20 bits of precision, we just scale the size of the input X to 40 bits.
The shifts are mostly straightforward calculations. The "(totalLen & 1)" is required to make sure we shift by an even amount. For example, the binary Sqrt of 10000 is 100. This result is simply a right shift by an even number. If we had Sqrt(0b100000) (aka 32), then the Sqrt is 0b101(aka 5), and this is not a simple right shift anymore. We just need to keep the input length an odd number in length.
Round-to-Nearest Integer Version / Adapter
The Sqrt functions here all round down to the nearest integer. This is the standard for integer functions. If the result of a sqrt function is 99.999999998, then it should be rounded down to 99. However, in some cases, rounding to the nearest integer is preferred. To do this, all that is needed is to calculate one extra bit of precision with the standard integer sqrt function. If that extra ends up being a '0', it would be rounded down, or if a '1' bit, then rounded up.
BigInteger SqrtNearestInt(BigInteger x)
{
x <<= 2; // left shift by 2
var result = SunsetQuestSqrt(x);
if (result & 1 == 1)
result++;
return (result >> 1); //right shift by 1
}Testing
Extensive testing has been done for this algorithm, and I believe all the errors have been removed. However, to guarantee correctness, the following can be added near the end of the sqrt function. It will have around a 10% performance cost.
// lets test the integer function: val = Sqrt(x)
BigInteger squared = val * val;
if (squared > x)
{
Console.WriteLine($"val^2 ({squared}) < x({x})");
throw new Exception("Sqrt function had internal error - value too high");
}
if ((squared + 2 * val + 1) <= x)
{
Console.WriteLine($"(val+1)^2({(squared + 2 * val + 1)}) >= x({x})");
throw new Exception("Sqrt function had internal error - value too low");
}A considerable amount of time was spent testing the integer sqrt. It ran for several days on a 32-thread 1950x Threadripper with no errors.
Tests include:
Verification 1: Common issues in the past number testing
Verification 2: Brute Force Testing (Zero and up) [Ran up to 3.4e11 or 237]
Verification 3: 2n + [-5 to +5] Testing
Verification 4: n[2 to 7] + [-2 to 2] Testing
Verification 5: n2 –[0,1] Testing – overlaps with Verification 4 but tests larger numbers
Verification 6: Random number testing
The amount of testing has been extensive, so hopefully, there are no errors, however, if any are found, please report them.
Java Version
I wanted to create a Java version since Java is one of the most used programming languages. I basically took the C# version and made some adjustments to it. My Java skills are minimal, so I'm sure more optimizations can be done. Using the Newton Plus, it is still about 15X-45X faster than the built-in Java BigInteger Sqrt for numbers between 64 bits and 10240 bits in length. The built-in Java version has the advantage of numbers under 64 bits in length since it can use private Java libraries. For numbers over 64 bits, Newton Plus is much faster, however, if we use private java BigInteger methods and MutableBigInteger, then we can achieve even greater performance.
Performance Chart
The points below represent an average score for random numbers of different sizes. The gray points are the performance of Java's Big Integer. The orange is this paper's Newton Plus. Each dot represents the average of two trials, where each trial was a loop of thousands to millions of tests.
Random Notes:
The yellow is the speed-up. It is just the NewtonPlus/JavasSqrt.
It is up to 50X (5000%) faster for numbers around 10240 bits in length. For larger numbers, I would expect this to be even higher, like the C# chart.
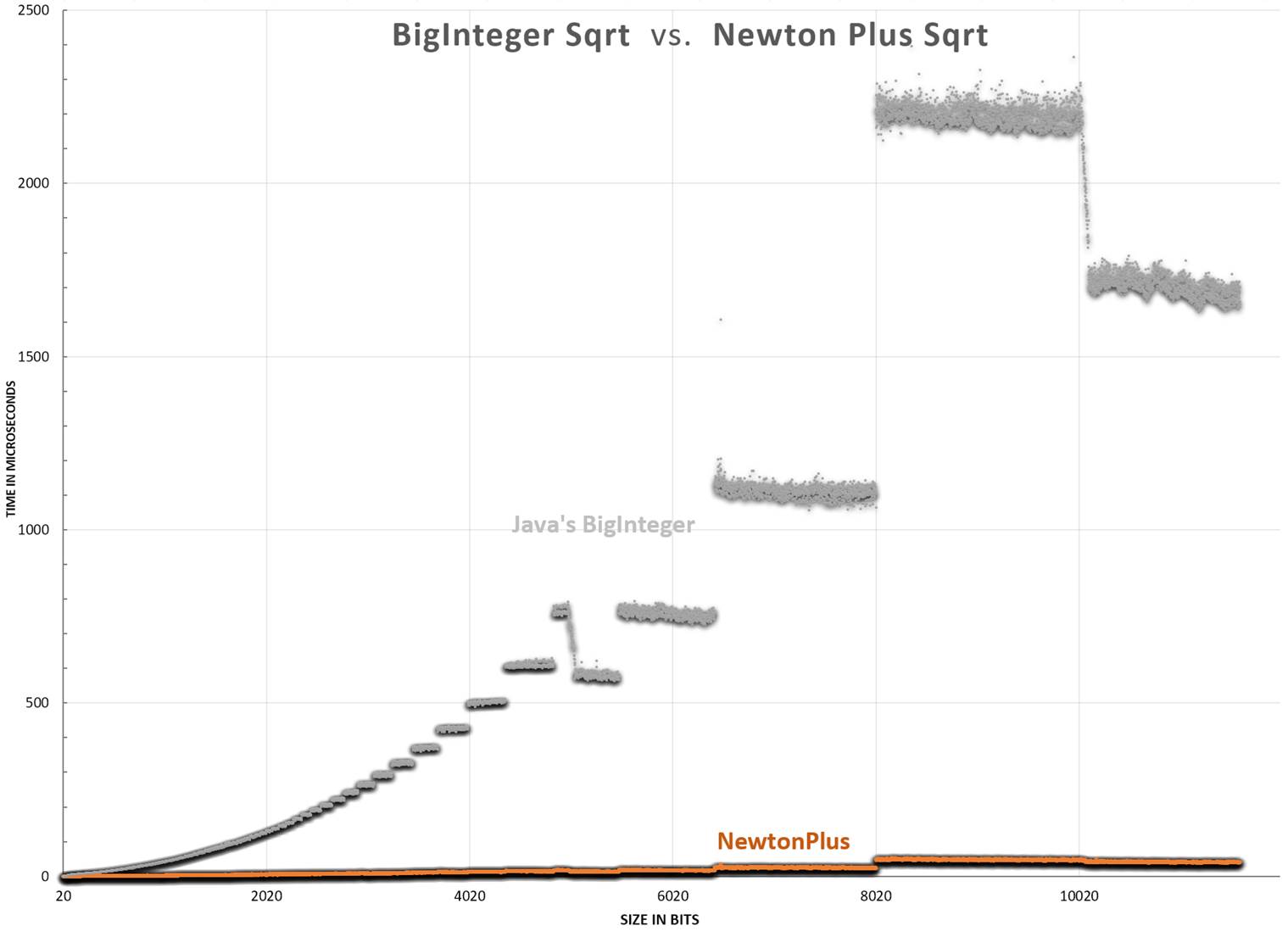
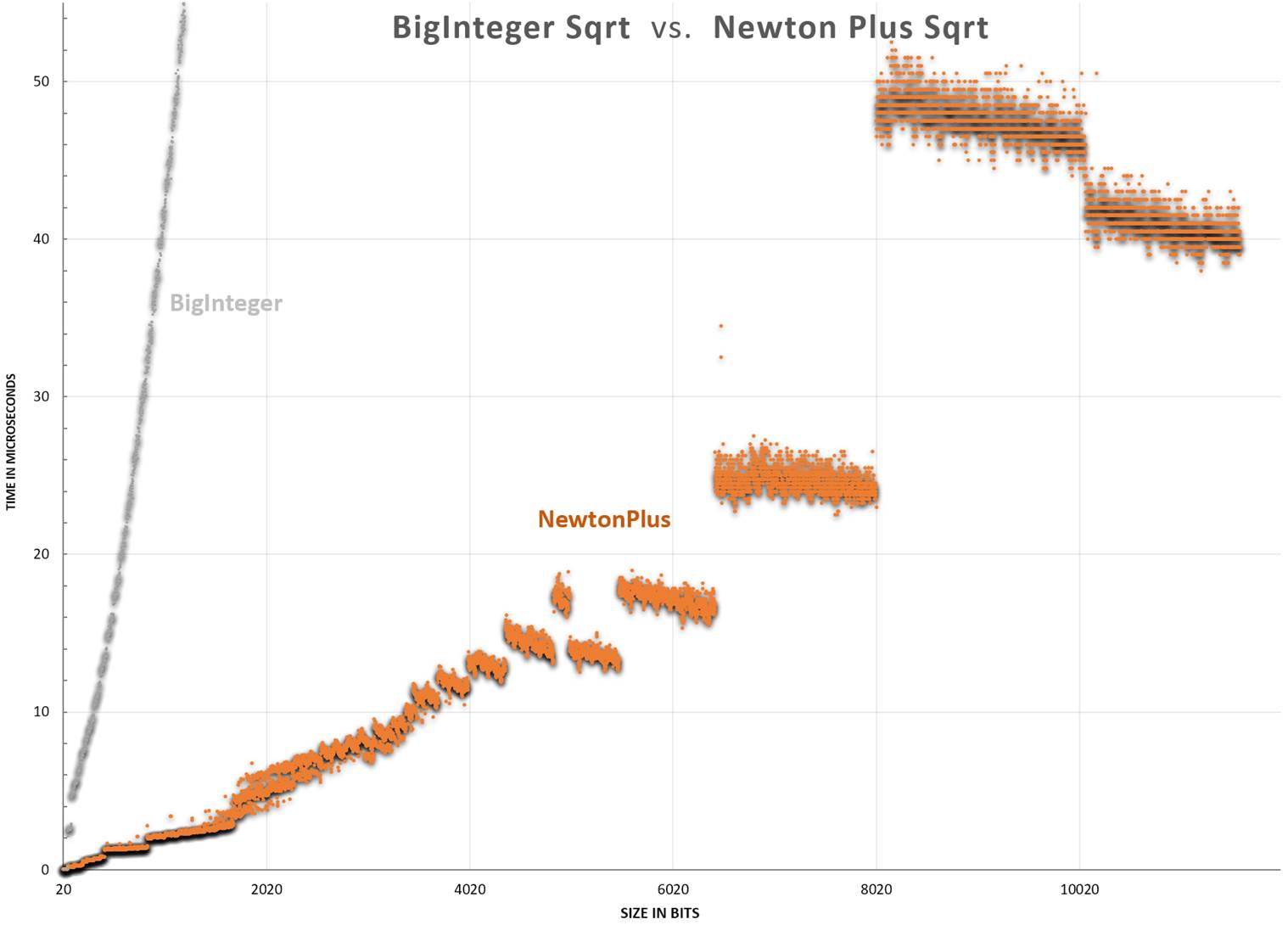Zoomed view for better detail
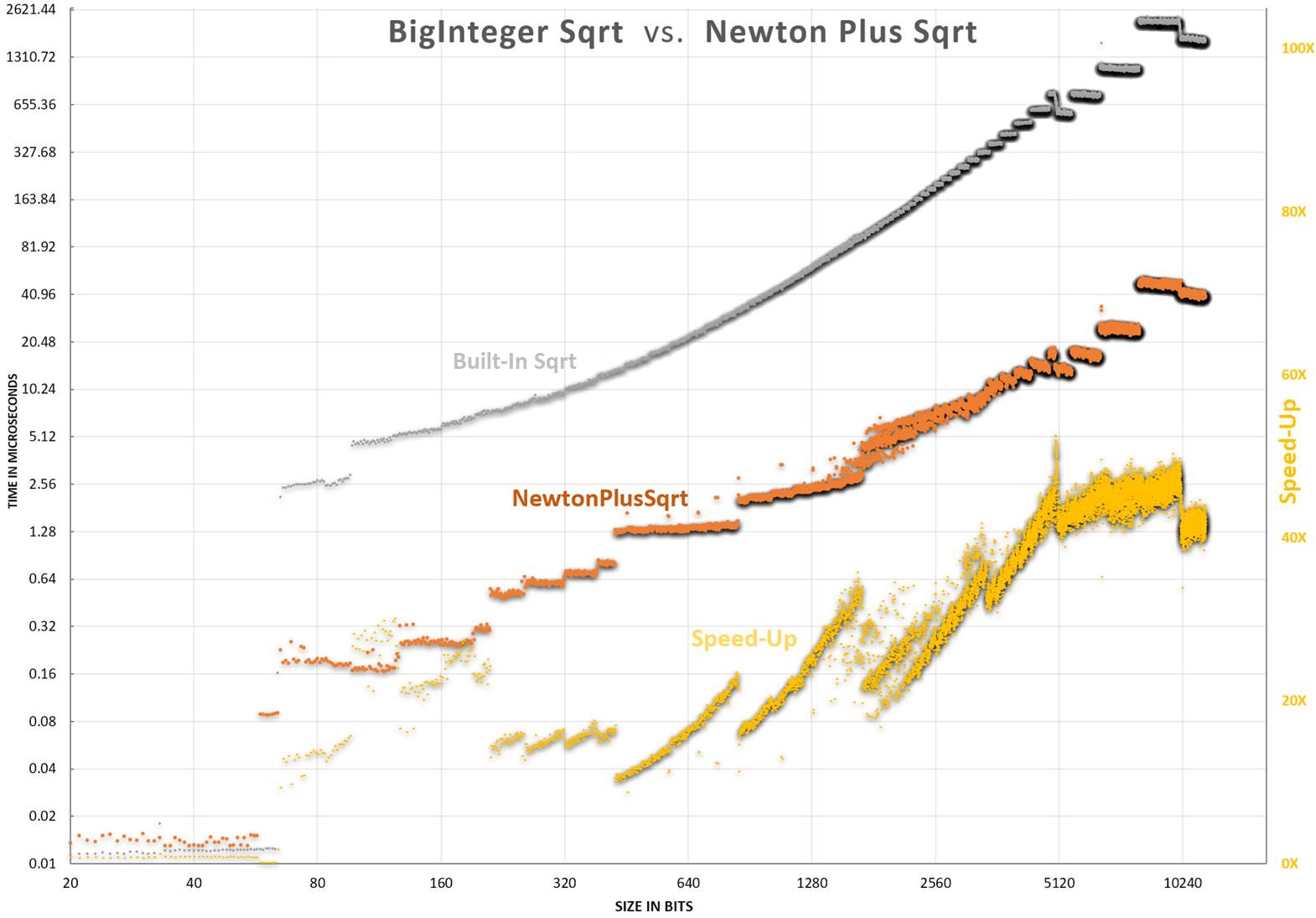Logarithmic view - each horizontal line represents a 2X performance gain. Yellow shows speed-up ratio.
The Code (Java Version)
public static BigInteger NewtonPlusSqrt(BigInteger x) {
if (x.compareTo(BigInteger.valueOf(144838757784765629L)) < 0) {
long xAsLong = x.longValue();
long vInt = (long)Math.sqrt(xAsLong);
if (vInt * vInt > xAsLong)
vInt--;
return BigInteger.valueOf(vInt); }
double xAsDub = x.doubleValue();
BigInteger val;
if (xAsDub < 2.1267e37) // 2.12e37 largest here since sqrt(long.max*long.max) > long.max
{
long vInt = (long)Math.sqrt(xAsDub);
val = BigInteger.valueOf((vInt + x.divide(BigInteger.valueOf(vInt)).longValue()) >> 1);
}
else if (xAsDub < 4.3322e127) {
// Convert a double to a BigInteger
long bits = Double.doubleToLongBits(Math.sqrt(xAsDub));
int exp = ((int) (bits >> 52) & 0x7ff) - 1075;
val = BigInteger.valueOf((bits & ((1L << 52)) - 1) | (1L << 52)).shiftLeft(exp);
val = x.divide(val).add(val).shiftRight(1);
if (xAsDub > 2e63) {
val = x.divide(val).add(val).shiftRight(1); }
}
else // handle large numbers over 4.3322e127
{
int xLen = x.bitLength();
int wantedPrecision = ((xLen + 1) / 2);
int xLenMod = xLen + (xLen & 1) + 1;
//////// Do the first Sqrt on Hardware ////////
long tempX = x.shiftRight(xLenMod - 63).longValue();
double tempSqrt1 = Math.sqrt(tempX);
long valLong = Double.doubleToLongBits(tempSqrt1) & 0x1fffffffffffff;
if (valLong == 0)
valLong = 1L << 53;
//////// Classic Newton Iterations ////////
val = BigInteger.valueOf(valLong).shiftLeft(53 - 1)
.add((x.shiftRight(xLenMod - (3 * 53))).divide(BigInteger.valueOf(valLong)));
int size = 106;
for (; size < 256; size <<= 1) {
val = val.shiftLeft(size - 1).add(x.shiftRight(xLenMod - (3 * size)).divide(val)); }
if (xAsDub > 4e254) // 4e254 = 1<<845.77
{
int numOfNewtonSteps = 31 - Integer.numberOfLeadingZeros(wantedPrecision / size) + 1;
// Apply Starting Size
int wantedSize = (wantedPrecision >> numOfNewtonSteps) + 2;
int needToShiftBy = size - wantedSize;
val = val.shiftRight(needToShiftBy);
size = wantedSize;
do {
//////// Newton Plus Iteration ////////
int shiftX = xLenMod - (3 * size);
BigInteger valSqrd = val.multiply(val).shiftLeft(size - 1);
BigInteger valSU = x.shiftRight(shiftX).subtract(valSqrd);
val = val.shiftLeft(size).add(valSU.divide(val));
size *= 2;
} while (size < wantedPrecision);
}
val = val.shiftRight(size - wantedPrecision);
}
// Detect a round ups. This function can be further optimized - see article.
// For a ~7% speed bump the following line can be removed but round-ups will occur.
if (val.multiply(val).compareTo(x) > 0)
val = val.subtract(BigInteger.ONE);
return val;
}World's Fastest Square Root for Big Numbers?
The World's fastest for Java and C#... I think so. But this project is not the world's fastest square root.
The fastest that I have found is the GMP Square Root. It is considerably faster. GMP/MPIR is likely faster because it is written in assembly and C – both low-level languages. When writing in asm/c, the hardware architecture can be used to its fullest, including SSE/AVX 128-bit instructions/registers, optimizing cache, and other close-to-metal tricks/instructions.
Here are some very rough comparisons: (in ns)
| Number Size | GMP (ns) | This Project (ns) | Speed-Up |
|---|---|---|---|
| 1E+77 | 350 | 1058 | 3.0X |
| 1E+154 | 650 | 2715 | 4.2X |
| 1E+308 | 1150 | 5330 | 4.6X |
| 1E+616 | 1650 | 7571 | 4.6X |
| 1E+1233 | 2450 | 14980 | 6.1X |
| 1E+2466 | 4250 | 35041 | 8.2X |
| 1E+4932 | 6650 | 121500 | 18X |
| 1E+9864 | 17650 | 458488 | 26X |
| 1E+19728 | 51850 | 1815669 | 35X |
| 1E+39457 | 144950 | 6762354 | 47X |
Optimizations
All this speedup is done with different optimizations, tricks, techniques, technologies, creative ideas, or whatever we want to call them. Each one of these ideas adds to the overall performance. The ideas here come from myself and others.
First off, let's review the basics. There are a few long-time-known methods of finding a square root, and the most popular is Newton's method (also known as the Babylonian method or Heron's method). It can be summarized into:
Let x = the number we want to find the sqrt of
Let v = a rough estimate of Sqrt(x)
while(desired_precision_not_met)
v = (v + x / v) / 2
return vWhen calculating a square root using Newton's method (and other methods), we start by finding the most significant digits. This first step can be done by choosing a number that is half the number of bits as the inputs. So, the number 2101 (a 1 with 101 zeros in binary) will have a good starting point of around 251. This roughly gets us started with one bit of accuracy at the correct scale.
Optimization: Shrinking the Division (Newton Plus)
When calculating Newton's method, the costliest part is the division. The division is time-consuming for computers and humans alike. If somehow this division can be shrunk, it would put us in a much better place regarding the work needed for the calculation.
When doing typical Newton iterations by hand in binary, something jumps out. The "v +" is just the previous iteration of v tacked on the front. Furthermore, these bits are already there, so we are just upshifting the top half by 1. If we already have these bits, do we really need to have them in the divide? Can we somehow remove this part since we have it already? The answer is they don't need to be in the divide.
The Code for Newton Plus
Below is one iteration of Newton Plus. This should be repeated until the desired precision is met.
void NewtonPlus(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
int shiftX = xLenMod - (3 * size);
BigInteger valSqrd = (val * val) << (size - 1);
BigInteger valSU = (x >> shiftX) - valSqrd;
val = (val << size) + (valSU / val);
size <<= 1;
}The parameters:
"X" is The input. The value we are trying to find the Sqrt of.
"xLenMod" is Len(X) rounded up to the next even number. It is just calculated once.
"size" is a maintained current size of val. This is so it does not need to be recalculated each time the method below is called. The size is also doubled when the method is called.
"val" is the current result. Each call to this function doubles the precision.
Just for comparison, here is a typical Newton:
void NewtonClassic(BigInteger x, int xLenMod, ref int size, ref BigInteger val)
{
BigInteger tempX = x >> xLenMod - (3 * size) + 1;
val = (val << (size - 1)) + tempX / val;
size <<= 1;
}Further Optimization Ideas
Here are additional optimization ideas for the rest of the world to work on:
How Did This Function Come About?
I needed a Big Integer square root function for a project I was working on. I looked around, found a few, and selected one I liked. The one I liked was not on a site I use called StackOverflow, so I re-posted it (with credit to the author/date). After some time passed, there was a post by MaxKlaxx. MaxKlaxx posted benchmarks comparing his and several others, including the one I re-posted as "SunsetQuest" – even though it was not mine. The one with Sunsetquest was one of the lowest performers, and if anyone knows much about me, I'm all about efficient code – duh! So, I decided to make my own sqrt function to see if I could take the lead.
Max's algorithm was fast from small to large integers, using the built-in hardware SQRT() for small numbers and as an initial guess for larger numbers combined with Newton iterations.
After several weeks of working on it here and there, I gave up and wrote, "THIS PROJECT WAS A DISASTER!!!!! 1/8/2021". But, after some time went by, ideas started bubbling up. The first one was basically trying to split the sqrt into smaller square roots. Long story short, that idea was a flop! But ideas kept flowing for some reason, usually in the middle of the night. With all these working together, the square root is super quick. This solution is 43X faster for larger numbers than the next fastest C# algorithm I could find.
History
3/14/2022: Initial version
7/1/2023: Fixed HTML rendering issues, general cleanup/grammar, and made examples easier to follow
2/2025: Enhanced with SunsetQuestSqrt for very large numbers
License
This article, along with any associated source code and files, is licensed under The MIT License.
Written By
Ryan Scott White
Ryan is an IT Coordinator, living in Pleasanton, California, United States